اختر الاجابة الصحيحة فيما يلي ( يكتفى بنقل رقم السؤال و الاجابة الصحيحة في كراسة الاجابة :
1) اذا كانت س ، ص > 0 ، 2س + 3ص = 30 حيث ق = س × ص فإن قيمتي س ، ص على الترتيب اللتين تجعلان ق اكبر ما يمكن هما على الترتيب :
أ)7.5 ، 5 ب) 3 ، 8 ج) 12 ،2 د) 6، 6
2) اذا كان فإن د(س) تساوي:
3)
أ) ب) ج) د)
4)
= أ) لو 5 - لو 1 ، ب) صفر ، ج) لو1 - لو5 د) لو 4
5) ( حيث هـ عدد حقيقي ثابت )
أ) 1419 هـ ب) 1351 هـ ج) 6595 هـ د) 1420 هـ
6) اذا كانت د متصلة على الفترة [ 1 ، 3 ] و كان د (1) = 5 ، د(3)=9 فإن:
أ)2 ب) -2 ج) 35 د) 4
7) حجم الجسم الدوراني الناتد من دوران المنطقة المحصورة بين المنحنى ص = س و محور السينات على الفترة [ 0 ، 3 ]= :
(أ) 6ط وحدة طول مكعبة (ب) 18ط وحدة طول مكعبة (ج) 9ط وحدة طول مكعبة (د) 3ط وحدة طول مكعبة
8) إذا قطعت قبة كروية ارتفاعها 10 سم من كرة قطرها 14 سم فإن مساحة القبة الكروية = :
أ- ب- ج- د-
9) اذا كانت جـ نقطة حرجة للدالة د ، وكانت
فإن النقطة ( جـ ، د( جـ) ):
أ) صغرى محلية ب) عظمى محلية ج)انقلاب د)الاصل
10) إذا كانت فإن =
أ) ب) ج) 2س د)
س 2 :
ثانيا:
اجب عن جميع الاسئلة التالية:
أ) أوجد القيم القصوى للدالة
في الفترة [-2 ، 0 ]
ب) (أ)إذا كانت د(س) متصلة على [0 ، 2] ، وقابلة للاشتقاق على الفترة (0، 2) بحيث :
د (0) = 0 ، د(1) = 1 ، د(2) = 1 فاثبت أنه يوجد :
1)جـ1 ( 0 ، 1 ) بحيث (جـ1)=1 (ارشاد : استفد من نظرية القيمة المتوسطة للتفاضل )
2) جـ2 (1 ، 2 ) بحيث (جـ2) =0 (ارشاد: استفد من نظرية رول )
ج) ج) ارسم المنحنى المتصل لدالة كثيرة الحدود المعرفة على ح والتي تحقق الشروط التالية :
1) د(2) = د(5) = 0 ، د(0) = 20 ، د(4) = 4 ، د(3) = 2 .
2) (س) < 0 عندما س >4 أو س < 2
3) (س)>0 عندما 2 < س < 4
4) (س) < 0 عندما س >3
5) (س)>0 عندما س < 3
موضحا خطوات الحل بالتفصيل
س 3 :
أ) أوجد دالة المسافة ف(ن) لجسيم يتحرك بسرعة عنمد الزمن ن ، اذا علمت أن ف(0)=6
ب) أوجد مشتقة الدالة
ج) اوجد التكاملات التالية:
1) 2) 3) 4)
س 4 :
أ) منشور حجمه 280سم3 ، قاعدته مربعة الشكل ، تميل أحرفه الجانبية على مستوى قاعدته زاوية قدرها 30ْ ، أحسب طول ضلع قاعدته عندما يكون طول حرفه الجانبي 10سم.
(ب) اسطوانة دائرية قائمة ، إذا كانت النسبة بين مساحتها الجانبية وحجمها تساوي 10:1 فأوجد :
1- طول نصف قطر قاعدتها 2- المساحة الكلية للاسطوانة عندما يكون ارتفاعها 40سم





 رد مع اقتباس
رد مع اقتباس
 )
) (س) ، ل 2 (س) دالتين أصليتين للدالة د(س) = 3س + 2 ، وكانت هـ (س) =
(س) ، ل 2 (س) دالتين أصليتين للدالة د(س) = 3س + 2 ، وكانت هـ (س) =  (س) -
(س) - 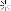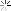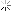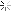


المفضلات